
This chapter discusses the behavior of automata with output, that is, finite-state operators. This repository puts the focus on finite state automata or finite state machines\parPublisher Summary. Diagrams like this visualize automata like a simple game. Would this be almost true for every m-state machineExample: Detect Even Number of 1s Jim Anderson (modified by Nathan Otterness) 2 This is a transition diagram for a deterministic finite automaton. Clearly, there exist m-state machines which can be built using only log m (take m 2 ) threshold cells. Efficient Simulation of Finite Automata by Neural Nets 497 On the other hand, every m-state Mealy machine can be built as a threshold machine (see Minsky 9, 10 or Section 5 in this paper).

You will find detailed descriptions (including the visuals) in this README file (if you scroll low enough to find what you came for)A finite automaton has a set of states and its control which moves it from state to state in response to external inputs. This repository is divided into more subfolders, each containing its own topic or automata that works in a particular manner F Q is the set of accept or final states Q0 Q is the start state, and 5.
Finite State Automata Even Number Of Code Class Is
That is why I decided to start with the implementation of a DFA that checks for parity (of number one) in a given binary string.This is what a translation of this program would sound in automata world: A transition function that will assing a next state to the current state, when a particular input arrives (in the code class is denoted TransitionFunction and a variable denoted delta)I believe it is important to start with a simple,direct (sometimes hardcoded) model and then to gradually expand the idea into a more general purpose program. A finite set of input symbols (in the code sometimes manually checked, sometimes denoted allowedInputs)

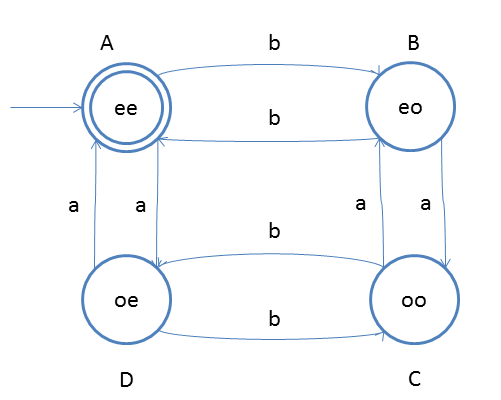
Four states -> even-even parity (accepted state), even-odd parity (not accepted state), odd-even parity (not accepted state), & odd-odd parity (not accepted state) Which does make sense when you think about it. Transition Function class - represents an entitiy that will be performing the transitions as inputs come along it contains a HashMap that should have defined key-value pairs for any key(input+current state token) -> value (next state)A bit more complex situation occures when we decide to build an automata that will check for both the parity of 1's and parity of 0's at the same time, given a binary string.Our number of total states grows exponentialy by a factor of two. State class - represents any state uniquely identified with a String 'name' also referenced as a 'token' of that state when performing transitions (token = id = name) A set of accepting states is a set containing only one state (even parity state)
A set of accepting states is a set containing only one state (even-even parity state)We use exactly the same classes as the previous example. Start state will be the accepted state (even-even parity) Same logic applies to all states. Being in that state and given an input of 1, we would transition to even-even state. So, even-odd state defines even number of 0's and odd number of 1's.
In this project, I made an automaton that is able to find a given combination of characters in a bigger input string. Regular expressions are meant to search for patterns, and therefore they have to be implemented to perform some sort of procedural scan of the entire input text. The concept arose in the 1950s when the American mathematician Stephen Cole Kleene formalized the description of a regular language. In this section, I will briefly explain how regular expressions work and what sorts of problems you might solve using them.A regular expression, also called regex, is usually thought of as a sequence of characters in a string or a text. They provide a variety of applications if used properly and in a smart way. Regular Expression AutomatonRegular expressions are very interesting topic to dive into and explore.
Start state has only two possible transitions, first one is a transition to the first state of the pattern (in this case state A), which occurrs give the input A, and a transition to itself for any other input. Now we have to define mappings (transitions) between our states. The start state represents any state that is not defined in our pattern. To explain a bit better, if we are looking to create an automaton that will search for a pattern "ABC", we need to create three states, state A,state B and state C. Each state represents a separate character.Each state also defines the transition to the next state, for a "correct" input.
All other states are mapped in a similar manner, only they also have to contain a transition to the first State of the pattern, in case we enter the lookup process and start anoter one midway through. It will also have transition to the start State for any other input.


 0 kommentar(er)
0 kommentar(er)
